如果简单平均法不舍弃某部分的历史数据，那么“陈旧”数据会影响到预测值，使预测值对现状不太敏感。，但是舍弃”陈旧“数据而只选取最新数据，固然可取，不过有时陈旧数据依然存在其应用价值，完全弃去又不全合适。那么平均移动就是对于这点进行改进。

移动平均法适用于即期预测。当产品需求既不快速增长也不快速下降，且不存在季节性因素时，移动平均法能有效地消除预测中的随机波动，是非常有用的。移动平均法根据预测时使用的各元素的权重不同，可以分为：简单移动平均和加权移动平均，以及指数移动平均。

移动平均法并不会对所有数据进行一次性的平均计算，而是选取一定的期数来进行移动的平均。当然这个期数越大，那么其值就会越接近平均法的计算结果，期数和平均法的所有数据完全相同时，实际上就是简单平均法了。移动平均法选择期数越短，预测对水平的反应就越强。

简单移动平均的公式：

是指t+1期的预测值

是t期的实际需求值，如此类推则是t-n+1期的实际需求值

是简单移动平均所包含的期数

采用过去三个月的历史数据进行移动平均的时候，计算方法和简单平均法一样，选取过去三个月的历史数据并除以期数得出三个月的平均值。当拥有2019年1月到3月的历史数据，通过三期移动平均法计算出1月到3月的平均值，并以此作为4月的预测值。当4月的实际需求值出现后，把它作为新的观测值加入而舍弃最早的观测数据。也就是说，舍弃1月的实际需求值，采用2月到4月的实际值作为计算依据了。

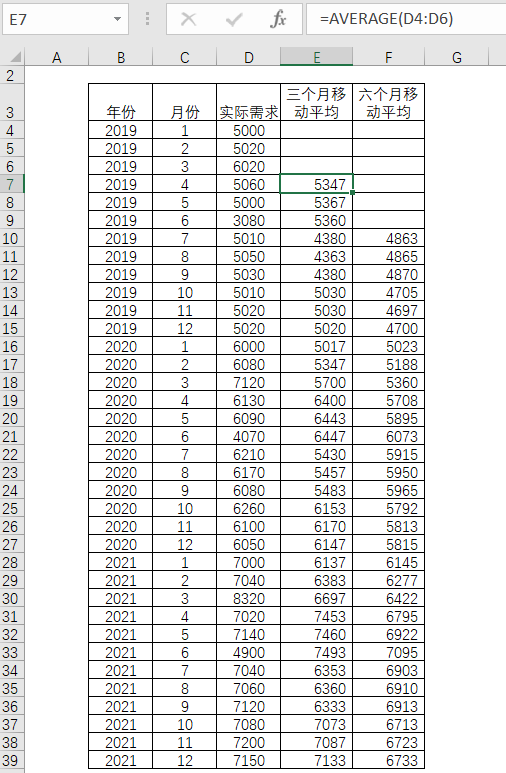
表4-6是选取3期和6期数据进行移动平均的比较。

表4-6 移动平均法的比较

再通过折线图进行对比:

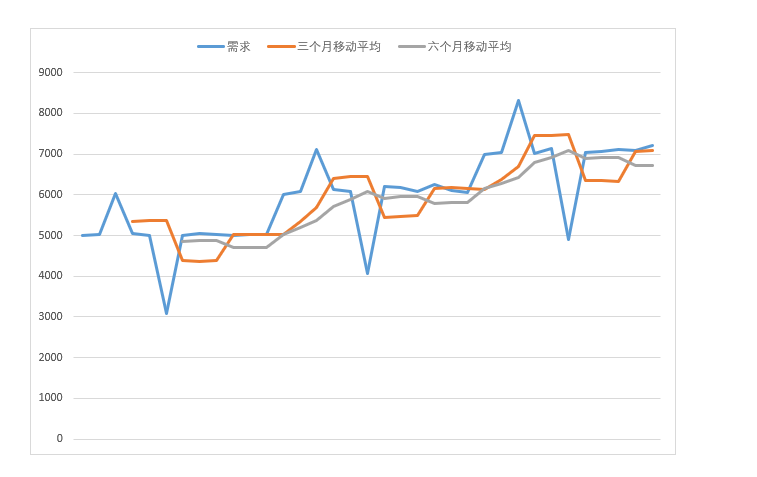
图4-7

通过图4-7的比较看出，三个月的移动平均比较能反映起伏，而6个月的移动平均，由于期数更多，消除了更多的起伏因素，从而显得变化更加平稳。移动平均法可以通过改变用以平均的周期的长短来调整敏感性，使用少量的数据的平均值得到的预测结果能够快速地响应需求的变化，但有可能变得过于敏感从而受到非典型数据和偶然波动性的影响。

这种移动平均法是简单的移动平均法，每一期的权重都是一致的。

不过对于预测来说，比起“陈旧”的信息，越接近现在的信息越值得信赖，为此，对于不同期数赋予不同的权重，其加权模式是从当前数据到之前的数据，依据线性递减的，从而通过加权方式来增强最新数据所起的作用。

如果采用四期数据来做加权移动平均，对于过去的四期数据，从最远的一期数据开始，分别赋予1，2，3，4的权重，藉此进行四期的移动平均。

表4-7 加权平均移动法

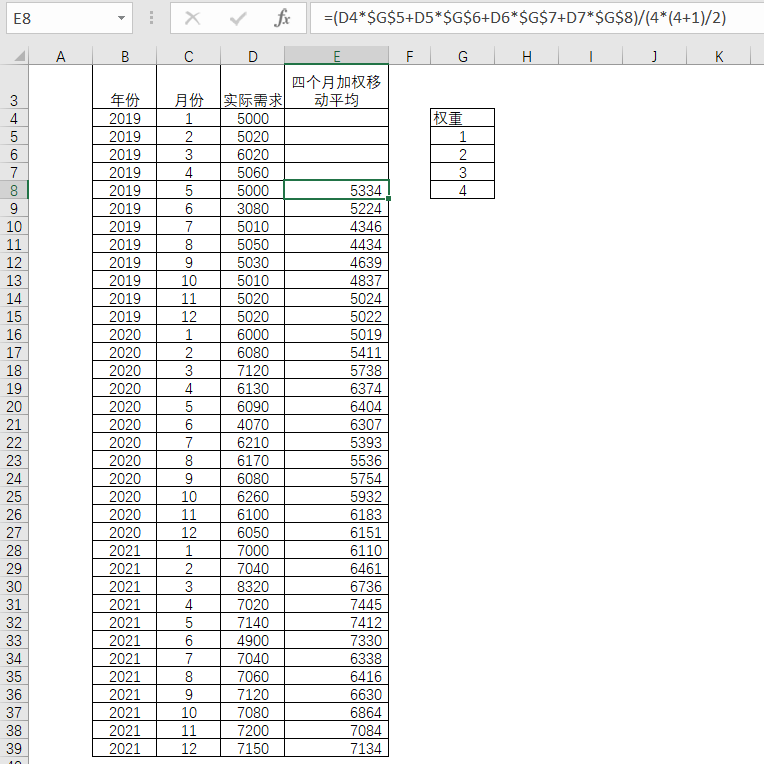
还有一个简便的方法就是直接赋予各期实际需求相应的权重比率，然后根据各自的乘积相加。权重的合计应当为1。

表4-8 加权平均移动法

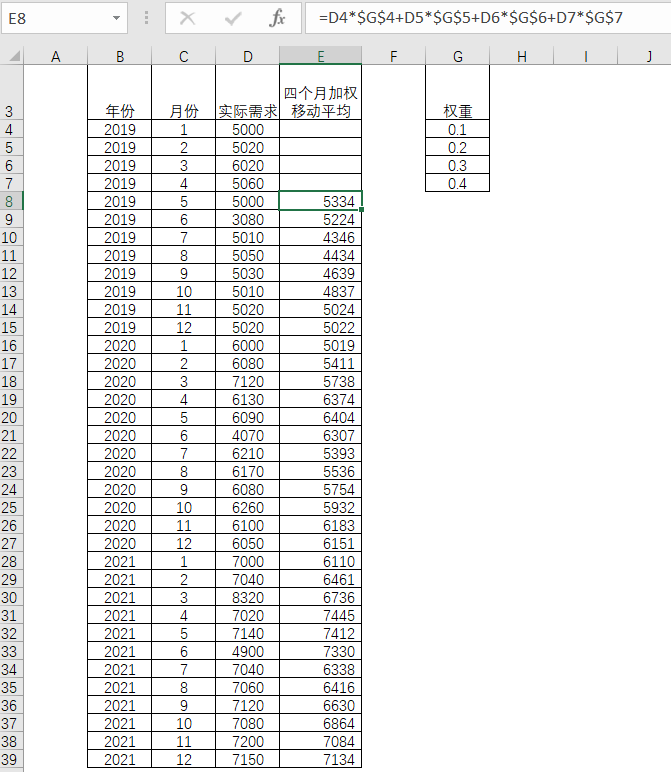
表4-8中虽然权重合计为1，不过并非一定要按照递进关系赋予各数据的权重，可以根据实际赋予不同期数的权重比例，比如采用三期数据的话，对应权重赋予为0.2，0.3和0.5。

移动平均，不管是简单移动平均抑或是加权移动平均，继承了简单平均法的特点外，还考虑了历史数据的新与旧，对于预测的影响力不同，而更多地把较新的历史数据作为重要的计算依据加入到计算当中。但是和简单平均法一样，当数据含有季节性因素，趋势时，移动平均还是有点缺陷，同样也会消除这些可能会在未来反映的因素，不过期数越短，消除得越少，还是多少把过去的规律一定程度地应用在未来预测上。如果数据只有水平和噪声因素的话，它只需要少量的数据并且能够把最新数据的敏感性反映出来。

移动平均法面临的问题是，应该选择多少期数据作为计算依据。