在很多实际问题上，变量之间并非都是线性关系，自变量和因变量之间往往存在某种曲线关系，这就是非线性关系。如果对此强行建立线性回归模型，那么就会影响预测的准确性了。

某网站各期浏览时间超10小时用户数和当期销售额关系，呈现非线性关系。

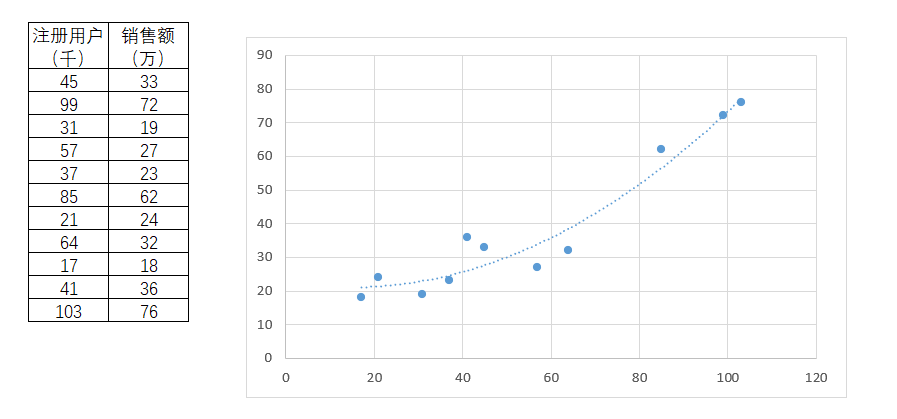
图4-45 非线性关系图

假如直接对此做线性回归，并以此回归方程，得出结果如图4-46，其R平方值为0.88044。

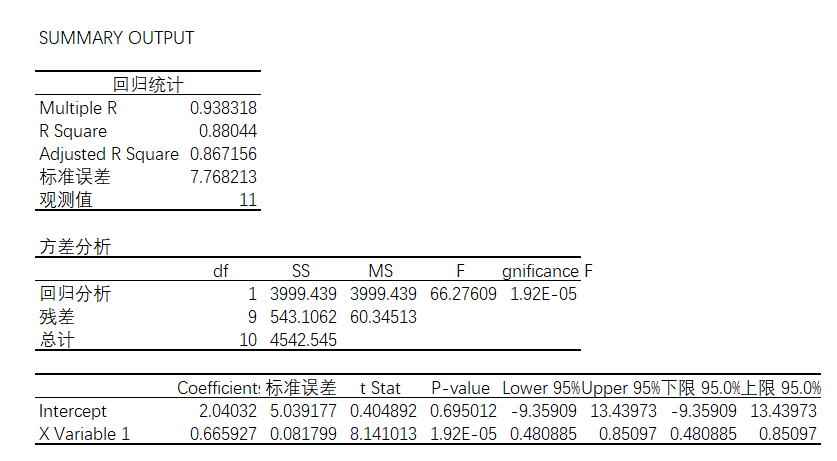
图4-46 线性回归分析结果

那么对于非线性的处理，可以通过变换自变量或/和因变量来建立非线性回归模型。虽然此时为非线性函数形式，但是模型中的参数认为是线性的。最常见的变换方式是对变量做自然对数变换，变为。当待变换的数值存在0的时候，要认为地对所有值加1，然后再进行变换，否则取值为0的数值在对数变换之后依然还是0。

本例对销售额使用Excel函数ln进行自然对数变换，结果保留两位小数点。

表4-51

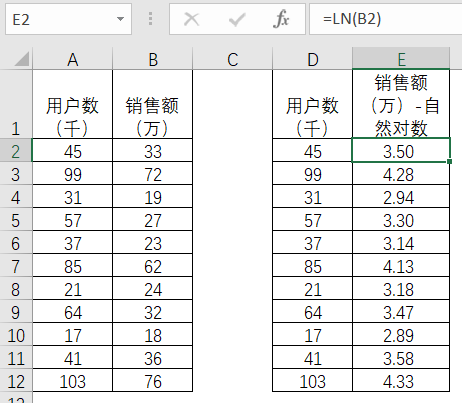
接着进行线性回归分析，得到R平方值为0.881613，比之前略有提高。

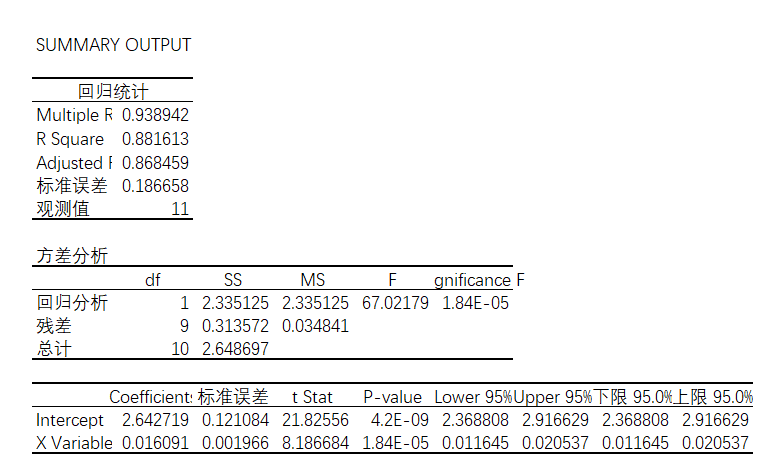
图4-47 线性回归分析结果

不过要注意的是，回归分析得到的y值(销售额)对数变换之后得到的，应该建立公式的时候应该变换回去，使用的Excel函数是Exp，得到值为14.05（保留两位小数）。

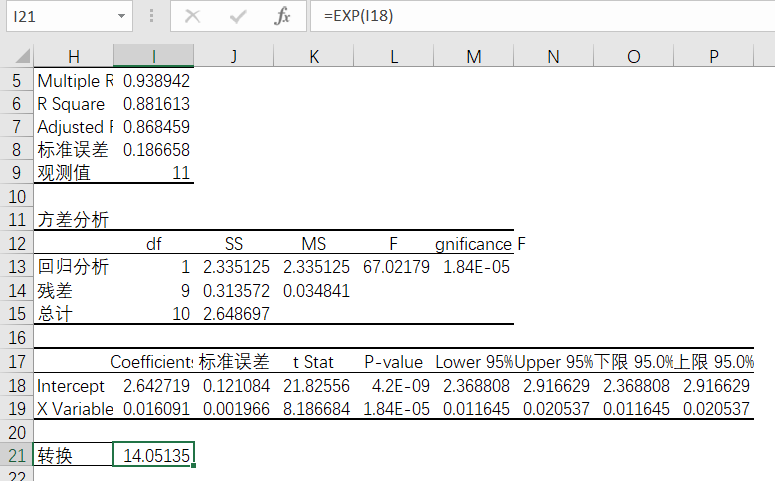
图4-48

因此线性方程公式就是

得到线性回归方程之后，只要有了下一期的用户数，那么就可以根据方程计算并预测同期的销售额。

然而有些时候，非线性转换为线性，其回归的拟合效果并不好。

如某商品的销售情况如下，呈现非常明显的曲线状态。

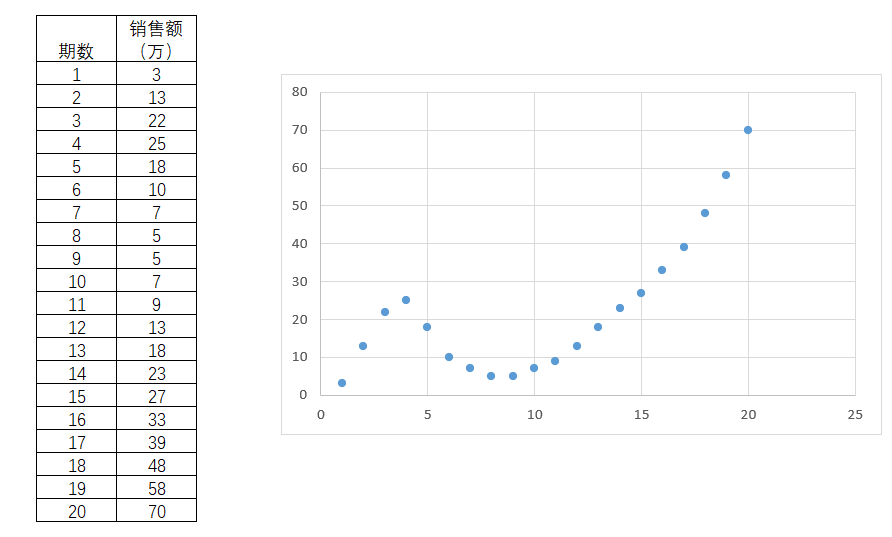
图4-49

这种情况下使用曲线估算，从中寻找出拟合度良好的曲线，建立非线性回归方程。其中SPSS软件，可以同时计算多种方法的曲线估计，如对数曲线、指数曲线、S曲线等来进行不同的尝试，进而能够寻找最佳的方程。

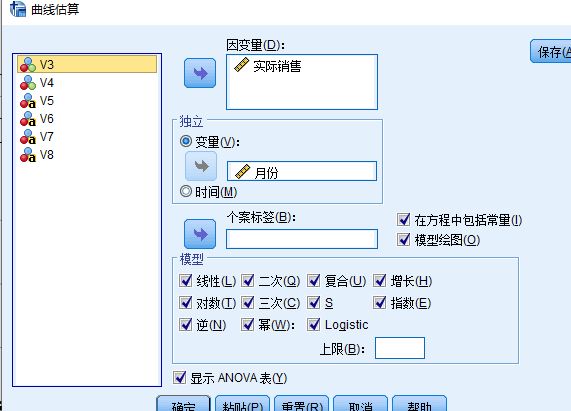
图4-50

当然，Excel也有一个简单的方法。直接在图示上添加对应的趋势线，从更多选项中，寻找并建立适合的曲线方程。

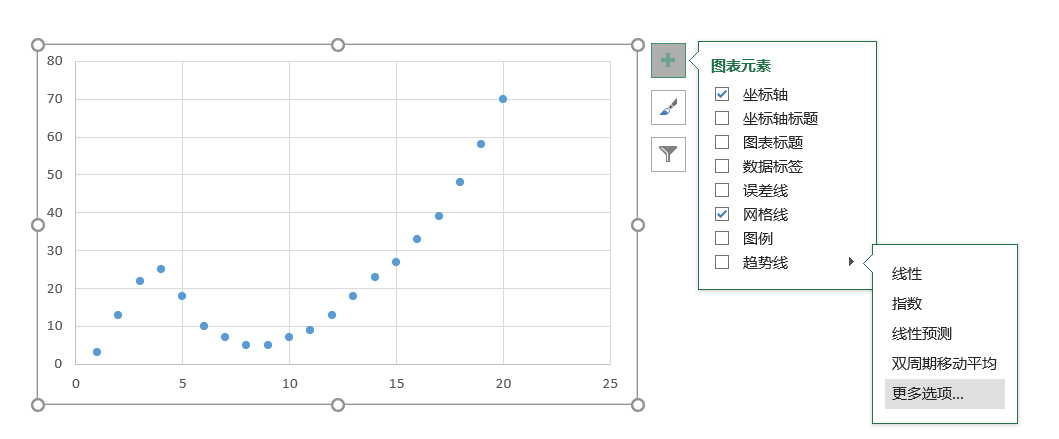
图4-51

当选择了4阶数的多项式趋势线，可以看到曲线呈现良好的拟合度，并且显示R平方值为0.9651。这意味着96.51%的响应变量变化可以用模型中的预测变量来解释。

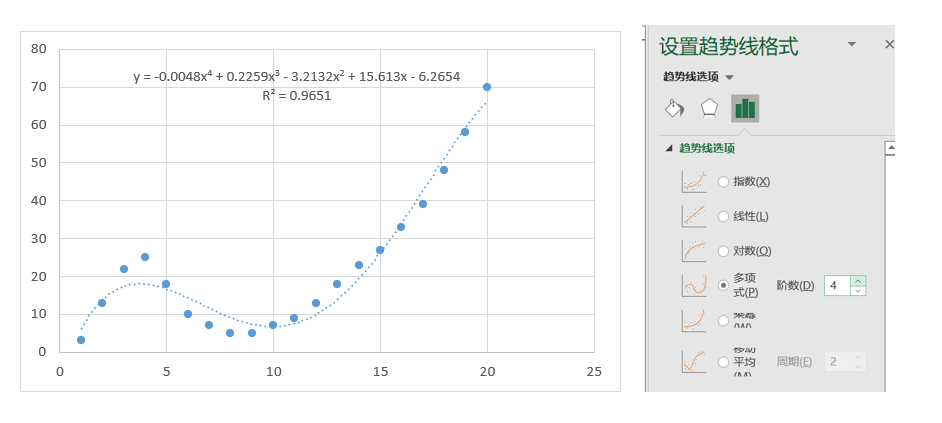
图4-52 4阶数的多项式趋势图

其公式为

因此就可以通过这个方程并对后续进行计算，用作预测。